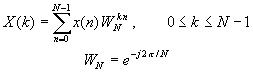
¡@
Fast Fourier Transform (FFT)
¡@
In this section we present several methods for computing the DFT efficiently. In view of the importance of the DFT in various digital signal processing applications, such as linear filtering, correlation analysis, and spectrum analysis, its efficient computation is a topic that has received considerable attention by many mathematicians, engineers, and applied scientists.
From this point, we change the notation that X(k), instead of y(k) in previous sections, represents the Fourier coefficients of x(n).
Basically, the computational problem for the DFT is to compute the sequence {X(k)} of N complex-valued numbers given another sequence of data {x(n)} of length N, according to the formula
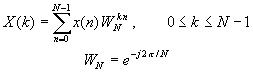
In general, the data sequence x(n) is also assumed to be complex valued. Similarly, The IDFT becomes
![]()
Since DFT and IDFT involve basically the same type of computations, our discussion of efficient computational algorithms for the DFT applies as well to the efficient computation of the IDFT.
We observe that for each value of k, direct computation of X(k) involves N complex multiplications (4N real multiplications) and N-1 complex additions (4N-2 real additions). Consequently, to compute all N values of the DFT requires N 2 complex multiplications and N 2-N complex additions.
Direct computation of the DFT is basically inefficient primarily because it does not exploit the symmetry and periodicity properties of the phase factor WN. In particular, these two properties are :
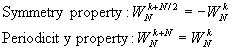
The computationally efficient algorithms described in this sectio, known collectively as fast Fourier transform (FFT) algorithms, exploit these two basic properties of the phase factor.
¡@
Radix-2 FFT Algorithms
Let us consider the computation of the N = 2v point DFT by the divide-and conquer approach. We split the N-point data sequence into two N/2-point data sequences f1(n) and f2(n), corresponding to the even-numbered and odd-numbered samples of x(n), respectively, that is,
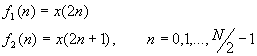
Thus f1(n) and f2(n) are obtained by decimating x(n) by a factor of 2, and hence the resulting FFT algorithm is called a decimation-in-time algorithm.
Now the N-point DFT can be expressed in terms of the DFT's of the decimated sequences as follows:
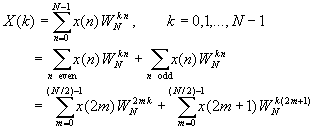
But WN2 = WN/2. With this substitution, the equation can be expressed as
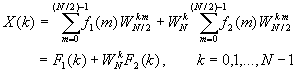
where F1(k) and F2(k) are the N/2-point DFTs of the sequences f1(m) and f2(m), respectively.
Since F1(k) and F2(k) are periodic, with period N/2, we have F1(k+N/2) = F1(k) and F2(k+N/2) = F2(k). In addition, the factor WNk+N/2 = -WNk. Hence the equation may be expressed as
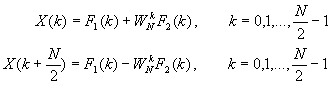
We observe that the direct computation of F1(k) requires (N/2)2 complex multiplications. The same applies to the computation of F2(k). Furthermore, there are N/2 additional complex multiplications required to compute WNkF2(k). Hence the computation of X(k) requires 2(N/2)2 + N/2 = N 2/2 + N/2 complex multiplications. This first step results in a reduction of the number of multiplications from N 2 to N 2/2 + N/2, which is about a factor of 2 for N large.
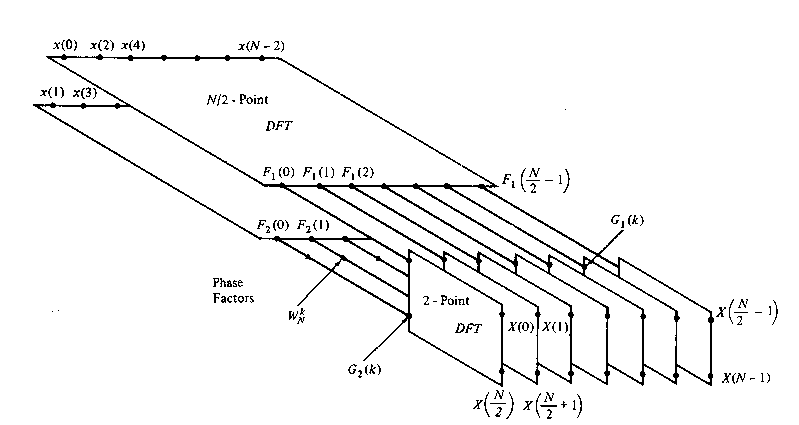
Figure TC.3.1 First step in the decimation-in-time algorithm.
¡@
By computing N/4-point DFTs, we would obtain the N/2-point DFTs F1(k) and F2(k) from the relations
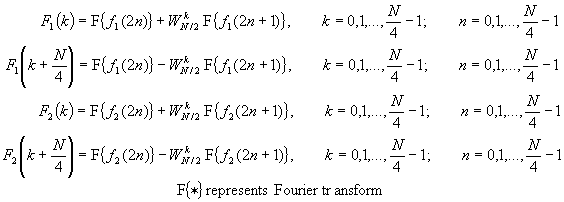
The decimation of the data sequence can be repeated again and again until the resulting sequences are reduced to one-point sequences. For N = 2v, this decimation can be performed v = log2N times. Thus the total number of complex multiplications is reduced to (N/2)log2N. The number of complex additions is Nlog2N.
For illustrative purposes, Figure TC.3.2 depicts the computation of N = 8 point DFT. We observe that the computation is performed in tree stages, beginning with the computations of four two-point DFTs, then two four-point DFTs, and finally, one eight-point DFT. The combination for the smaller DFTs to form the larger DFT is illustrated in Figure TC.3.3 for N = 8.
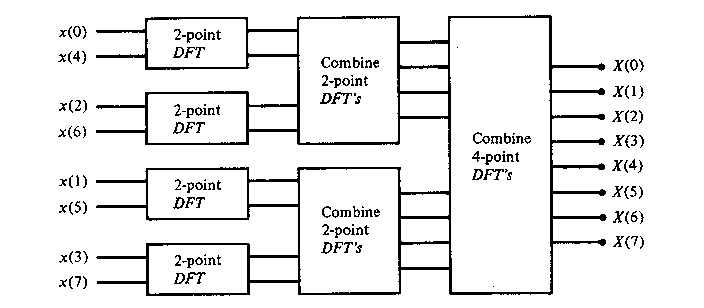
Figure TC.3.2 Three stages in the computation of an N = 8-point DFT.
¡@
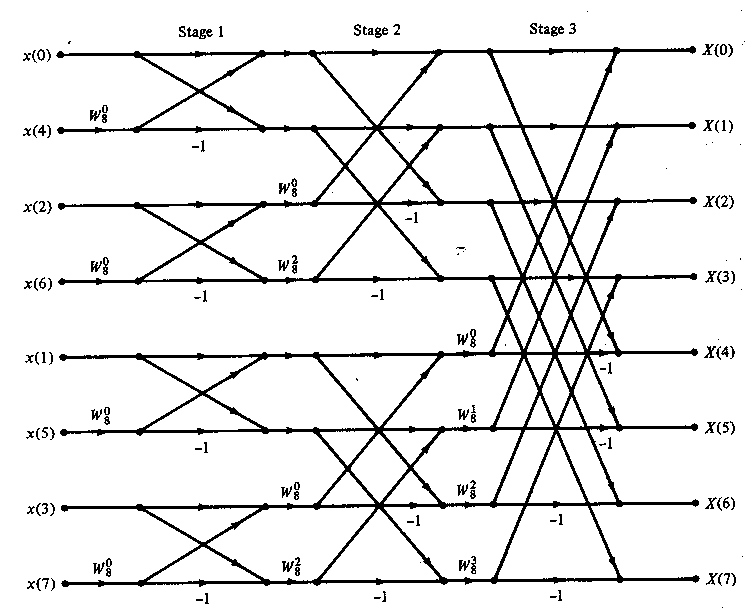
Figure TC.3.3 Eight-point decimation-in-time FFT algorithm.
¡@
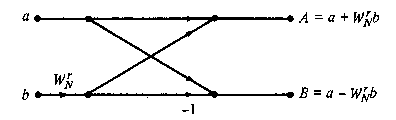
Figure TC.3.4 Basic butterfly computation in the decimation-in-time FFT algorithm.
¡@
An important observation is concerned with the order of the input data sequence after it is decimated (v-1) times. For example, if we consider the case where N = 8, we know that the first decimation yeilds the sequence x(0), x(2), x(4), x(6), x(1), x(3), x(5), x(7), and the second decimation results in the sequence x(0), x(4), x(2), x(6), x(1), x(5), x(3), x(7). This shuffling of the input data sequence has a well-defined order as can be ascertained from observing Figure TC.3.5, which illustrates the decimation of the eight-point sequence.
¡@
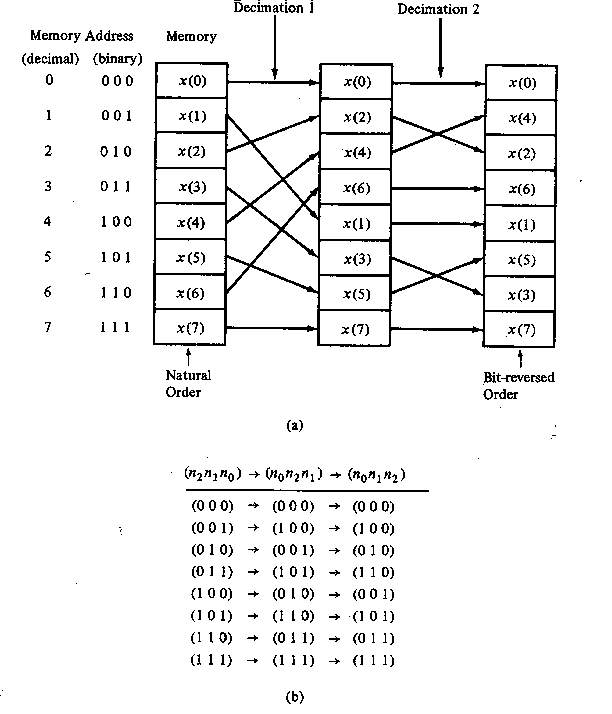
Figure TC.3.5 Shuffling of the data and bit reversal.
¡@
Another important radix-2 FFT algorithm, called the decimation-in-frequency algorithm, is obtained by using the divide-and-conquer approach. To derive the algorithm, we begin by splitting the DFT formula into two summations, one of which involves the sum over the first N/2 data points and the second sum involves the last N/2 data points. Thus we obtain
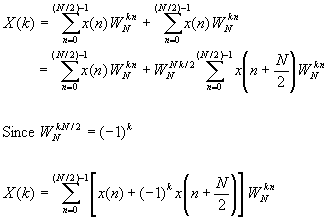
Now, let us split (decimate) X(k) into the even- and odd-numbered samples. Thus we obtain
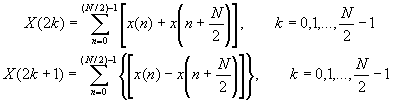
where we have used the fact that WN2 = WN/2
The computational procedure above can be repeated through decimation of the N/2-point DFTs X(2k) and X(2k+1). The entire process involves v = log2N stages of decimation, where each stage involves N/2 butterflies of the type shown in Figure TC.3.7. Consequently, the computation of the N-point DFT via the decimation-in-frequency FFT requires (N/2)log2N complex multiplications and Nlog2N complex additions, just as in the decimation-in-time algorithm. For illustrative purposes, the eight-point decimation-in-frequency algorithm is given in Figure TC.3.8.
¡@
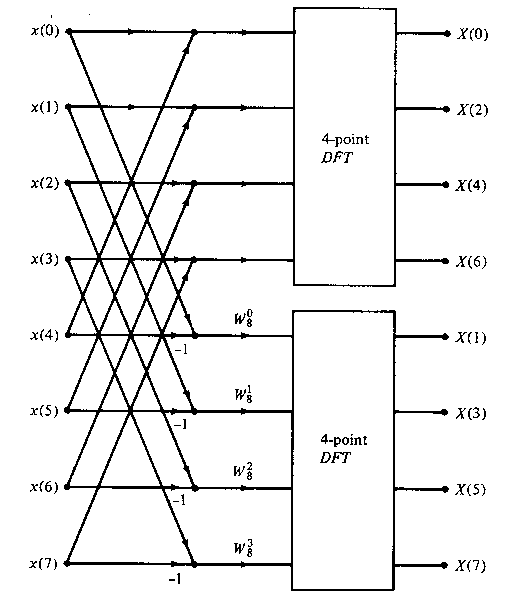
Figure TC.3.6 First stage of the decimation-in-frequency FFT algorithm.
¡@
¡@
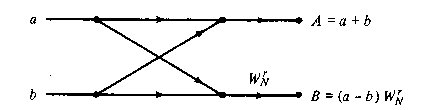
Figure TC.3.7 Basic butterfly computation in the decimation-in-frequency.
¡@
¡@
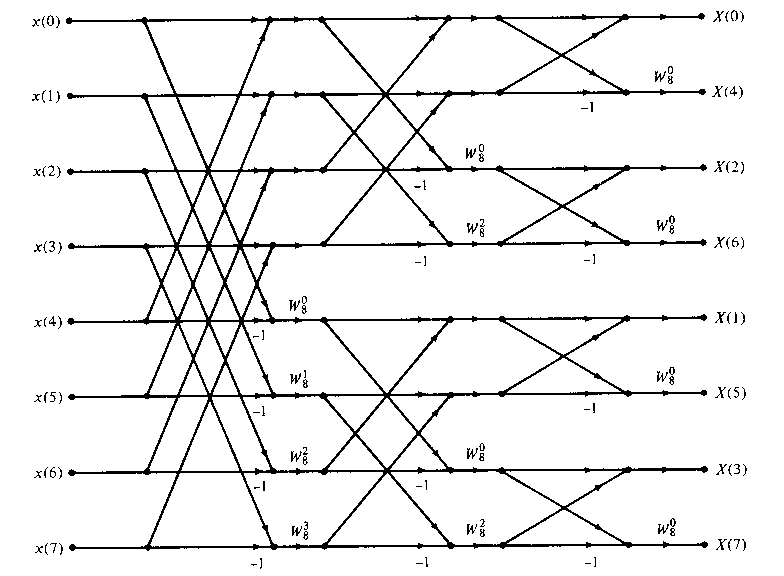
Figure TC.3.8 N = 8-piont decimation-in-frequency FFT algorithm.
¡@
We observe from Figure TC.3.8 that the input data x(n) occurs in natural order, but the output DFT occurs in bit-reversed order. We also note that the computations are performed in place. However, it is possible to reconfigure the decimation-in-frequency algorithm so that the input sequence occurs in bit-reversed order while the output DFT occurs in normal order. Furthermore, if we abandon the requirement that the computations be done in place, it is also possible to have both the input data and the output DFT in normal order.
¡@
Radix-4 FFT Algorithm
When the number of data points N in the DFT is a power of 4 (i.e., N = 4v), we can, of course, always use a radix-2 algorithm for the computation. However, for this case, it is more efficient computationally to employ a radix-r FFT algorithm.
Let us begin by describing a radix-4 decimation-in-time FFT algorithm briefly. We split or decimate the N-point input sequence into four subsequences, x(4n), x(4n+1), x(4n+2), x(4n+3), n = 0, 1, ... , N/4-1.
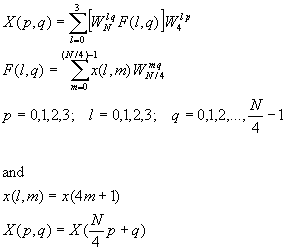
Thus the four N/4-point DFTs F(l, q)obtained from the above equation are combined to yield the N-point DFT. The expression for combining the N/4-point DFTs defines a radix-4 decimation-in-time butterfly, which can be expressed in matrix form as
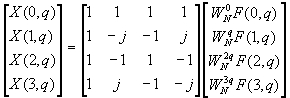
The radix-4 butterfly is depicted in Figure TC.3.9a and in a more compact form in Figure TC.3.9b. Note that each butterfly involves three complex multiplications, since WN0 = 1, and 12 complex additions.
¡@
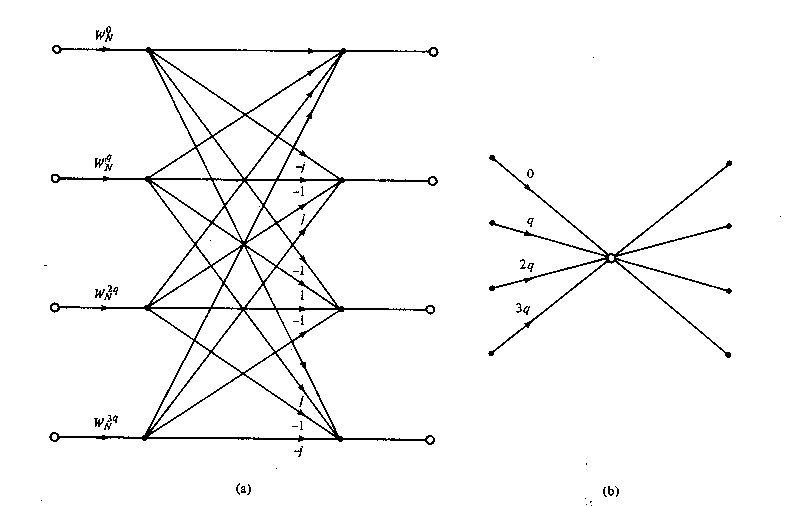
Figure TC.3.9 Basic butterfly computation in a radix-4 FFT algorithm.
¡@
By performing the additions in two steps, it is possible to reduce the number of additions per butterfly from 12 to 8. This can be accomplished ty expressing the matrix of the linear transformation mentioned previously as a product of two matrices as follows:
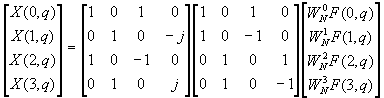
¡@
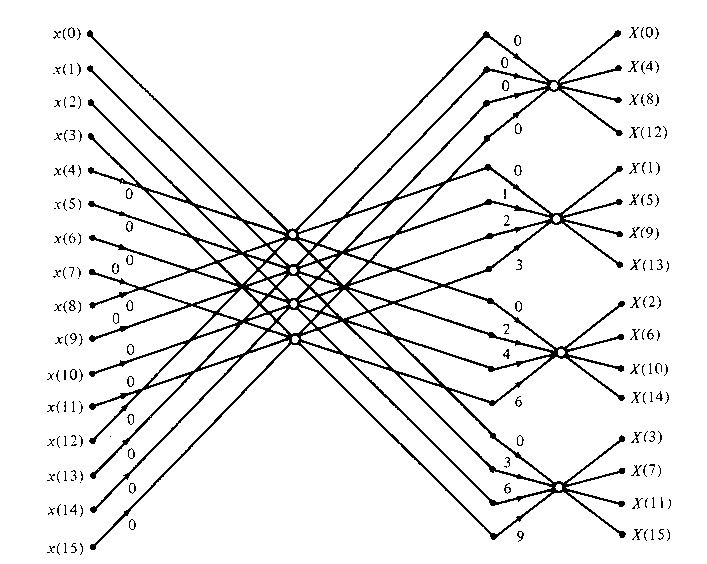
Figure TC.3.10 Sixteen-point radix-4 decimation-in-time algorithm with input in normal order and output in digit-reversed order
¡@
A 16-point, radix-4 decimation-in-frequency FFT algorithm is shown in Figure TC.3.11. Its input is in normal order and its output is in digit-reversed order. It has exactly the same computational complexity as the decimation-in-time radex-4 FFT algorithm.
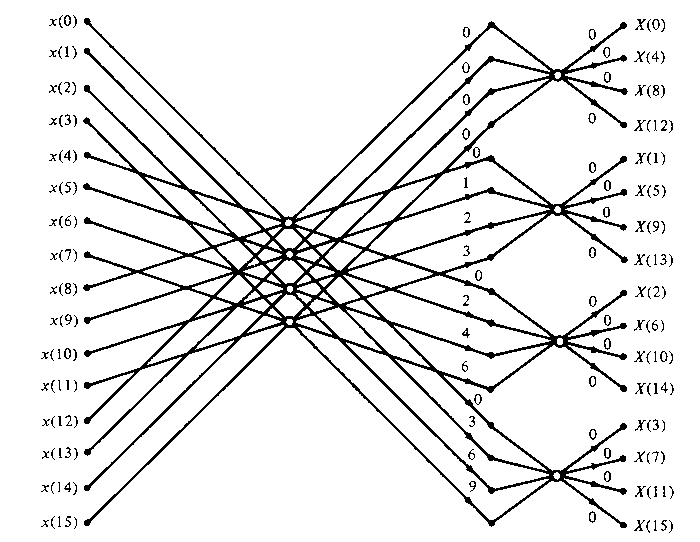
Figure TC.3.11 Sixteen-point, radix-4 decimation-in-frequency algorithm with input in normal order and output in digit-reversed order.
¡@
For illustrative purposes, let us re-derive the radix-4 decimation-in-frequency algorithm by breaking the N-point DFT formula into four smaller DFTs. We have
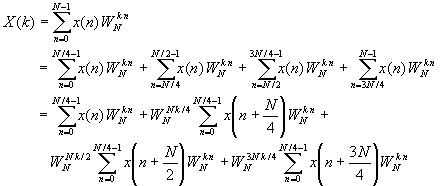
From the definition of the twiddle factors, we have
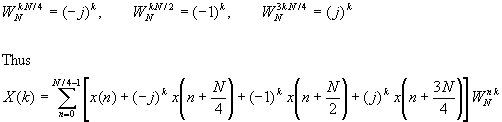
The relation is not an N/4-point DFT because the twiddle factor depends on N and not on N/4. To convert it into an N/4-point DFT we subdivede the DFT sequence into four N/4-point subsequences, X(4k), X(4k+1), X(4k+2), and X(4k+3), k = 0, 1, ..., N/4. Thus we obtain the radix-4 decimation-in frequency DFT as
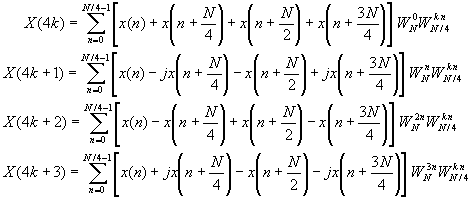
where we have used the property WN4kn = WknN/4. Note that the input to each N/4-point DFT is a linear combination of four signal samples scaled by a twiddle factor. This procedure is repeated v times, where v = log4N.
¡@
¡@
Split-Radix FFT Algorithms
An inspection of the radix-2 decimation-in-frequency flowgraph shown in Figure TC.3.8 indicates that the even-numbered pints of the DFT can be computed independently of the odd-numbered points. This suggests teh possibility of using different computational methods for independent parts of the algorithm, with the objective of reducing the number of computations. The split-radix FFT (SRFFT) algorithms exploit this idea by using both a radix-2 and a radix-4 decomposition in the same FFT algorithm.
First, we recall that in the radix-2 decimation-in-frequency FFT algorithm, the even-numbered samples of the N-point DFT are given as
![]()
A radix-2 suffices for this computation.
The odd-numbered samples {X(2k+1)} of the DFT require the pre-multiplication of the input sequence with the twiddle factors WNn. For these samples a radix-4 decomposition produces some computational efficiency because the four-point DFT has the largest multiplication-free butterfly. Indeed, it can be shown that using a radix greater than 4 does not result in a significant reduction in computational complexity.
If we use a radix-4 decimation-in-frequency FFT algorithm for the odd-numbered samples of the N-point DFT, we obtain the following N/4-point DFTs:
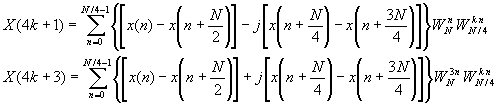
Figure TC.3.12 shows the flow graph for an in-place 32-point decimation-in-frequency SFFT algorithm.

Figure TC.3.12 Length 23 split-radix FFT algorithms from paper by Duhamel (1986); reprinted with permission from the IEEE
¡@
¡@
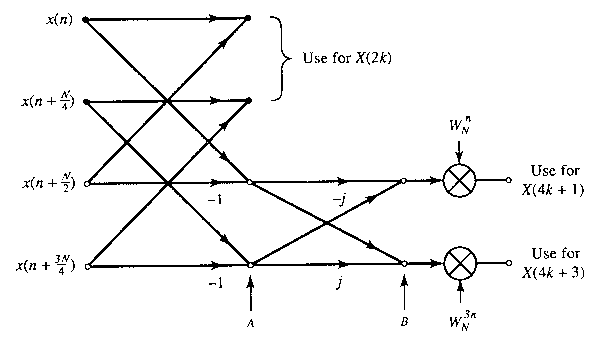
Figure TC.3.13 Butterfly for SRFFT algorithm.
¡@
¡@
| ¡@ | Real Multiplications | Real Additions | ||||||
| N | Radix-2 | Radix-4 | Radix-8 | Split Radix | Radix-2 | Radix-4 | Radix-8 | Split Radix |
| 16 | 24 | 20 | ¡@ | 20 | 152 | 148 | ¡@ | 148 |
| 32 | 88 | ¡@ | ¡@ | 68 | 408 | ¡@ | ¡@ | 388 |
| 64 | 264 | 208 | 204 | 196 | 1032 | 976 | 972 | 964 |
| 128 | 72 | ¡@ | ¡@ | 516 | 2054 | ¡@ | ¡@ | 2308 |
| 256 | 1800 | 1392 | ¡@ | 1284 | 5896 | 5488 | ¡@ | 5380 |
| 512 | 4360 | ¡@ | 3204 | 3076 | 13566 | ¡@ | 12420 | 12292 |
| 1024 | 10248 | 7856 | ¡@ | 7172 | 30728 | 28336 | ¡@ | 27652 |
Table TC.3.1 Number of Nontrivial Real Multiplcations and Additions to Compute an N-point Complex DFT