Encoding Process

Overview

 

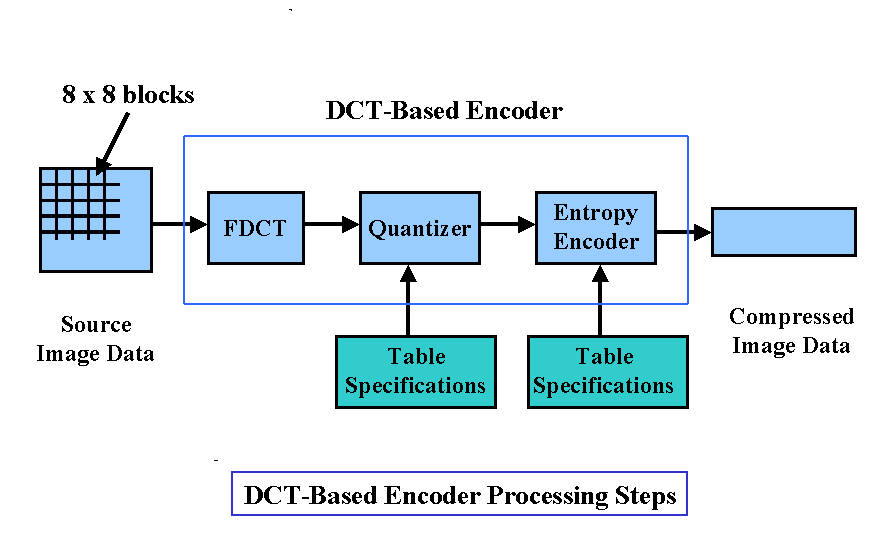
Now we begin to introduce more detail about the DCT-based modes of encoding operation. The following figure shows the key processing steps of encoding. It illustrates the special case of grayscale image compression.

 

Change color space

 Because of the high correlation among three components of RGB, the first step is usually to change color space from RGB space to YCbCr space. Generally speaking, eyes are more sensitive to illumination and less sensitive to saturation. Therefore, it can save storage by keeping more illumination data and less saturation data.

 

Discrete Cosine Transform (DCT)

After changing color space, source image samples are grouped into 8x8 blocks, shifted from unsigned integers to signed integers and input to the DCT. The following equation is the idealized mathmatical definition of the 8x8 DCT :

 

Each 8x8 block of source image samples is effectively a 64-point discrete signal which is a function of the two spatial dimensions x and y. The DCT takes such a signal as its input and decomposes of the 64 unique two-dimensional "spatial frequencies" which comprise the input signal's "spectrum." The ouput of the DCT is the set of 64 basis-signal amplitudes ( DCT coefficients ) whose values can be regarded as the relative amount of the 2D spatial frequencies contained in the 64-pint unput signal.

The DCT coefficients are divided into "DC coefficient" and "AC coefficients". DC coefficient is the coefficient with zero frequency in both dimensions, and AC coefficients are remaining 63 coefficients with non-zero frequences. The DCT step can concentrate most of the signal in the lower spatial frequencies. In others words, most of the spatial frequences have zero or near-zero amplitude and need not be encoded.

Because the DCT equations contain transcendental functions, no physical implementation can compute them with perfect accuracy. Besides, JPEG does not specify unique DCT algorithm in its propsed standard. This , however, makes compliance more difficult to confirm since two compliant encoders ( or decoders ) generally will not produce identical outputs given identical inputs.

 

Quantization

To achieve further compresesion, each of the 64 DCT coefficients is uniformly quantized in conjunction with a 64-element Quantization Table, which is specified by the application. The purpose of quantization is to discard information which is not visually significant.. Because quantization is a many-to-one mapping, it is fundamentally lossy. Moreover, it is the principal source of lossiness in DCT-based encoder.

Quatization is defined as division of each DCT coefficient by its corresponding quantizer step size, followed by rounding to the nearest integer, as following equation :

and then the output is normailized by the quantizer step size.

Each step size of quantization ideally should be chosen as the perceptual threshold to compress the image as much as poissible without visible artifacts. It is also a function of the source image characteristeics, display characteristics and viewing distance.

 

Entropy Coding

The final processing step of encoder is entropy coding. Before entropy coding, there are a few processing steps for the quantized coefficients. Note that  the DC coefficient is treated separately from the 63 AC coefficients.

The DC coefficients is a measure of the average value of the 64 image samples. Because there is usually strong correlation between the DC codfficients of adjacent 8x8 blocks, the quantized DC coefficient is encoded as the difference from the DC term of the previous block in the encoding order, called Differential Pulse Code Modulation ( DPCM ), and the function is as followed :

DiffDC(i) = DC(i) - DC(i-1)

where i is the i-th block, DC(0) = 0

DPCM can usually achieve further compression due to the smaller range of the coefficient values.

The remaining AC coefficients are ordered into the "zig-zag" sequence, which helps to facilitate entropy coding by placing low-frequency coefficients before high-frequency coefficients.

Now the outputs of DPCM and "zig-zag" scanning can be encoded by entropy coding seperately. It encodes the quantized DCT coeffieicts more compactly based on their statistical characteristics. The JPEG proposal specifies two entropy coding methods : Huffman coding and arithmetic coding.

Entropy coding can be considered as 2-step process. The first step converts the zig-zag sequnce of quantized coefficients into an intermediate sequence of symbols. The second step converts the symbols to a data stream in which the symbols no longer have externally identifiable boundaries. The form and definition of the intermediate symbols is dependent on both the DCT-based mode of operation and the entropy coding method.

 

JPEG Introduction