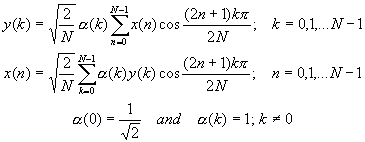
Discrete Cosine Transform (DCT)
¡@
The DCT is an orthonormal transform
y = Cx ; x = C-1y
defined by [Ahmed, Natarajan and Rao, 1974] [Ahmed and Rao, 1975]
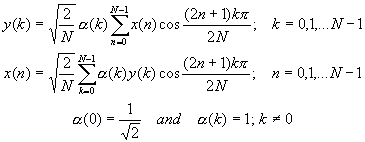
Note that correct to a
scaling factor, forward and backward (inverse) transforms have
identical transformation kernels. The last equation shows that
the basis vectors are sampled cosines which have phase shifts
that are not given by an alternating 0 and ![]() pattern as in
(the sines and cosines of) DFT. The DCT basis vectors are
pattern as in
(the sines and cosines of) DFT. The DCT basis vectors are
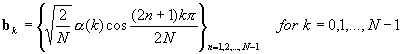
The attractiveness of the DCT is two-fold : (a) it is nearly optimal with high positive values of adjacent-sample correlation, and (b) it can be computed via the DFT using an FFT algorithm [Ahmed and Rao, 1975] [Chen, Smith and Fralick, 1976] [Elliott and Rao, 1982].
The fast computation procedure mentioned in (b) consists of extending the input block of N samples to a 2N-block with even symmetry, taking a 2N-point DFT, and saving N terms in it. The DFT of a real and symmetric sequence contains only real coefficients corresponding to the cosine terms of the series. The extension is defined as
![]()
as shown in Figure TC.3.1.1. The 2N-DFT of x'(n) is
![]()
By comparing it with y(k), it can be seen that
![]()
Notice that periodic extensions which are inherent in DFT operations have smaller end-effects (caused by discontinuity at the border of one block and its repetition) in the case of the 2N-extension than DFT operations based on the N-block. In DFT, quanization effects case an exchange of distortion components between the left and right boundaries. In DCT, such an exchange does not occur [Tribolet and Crochiere, 1979].
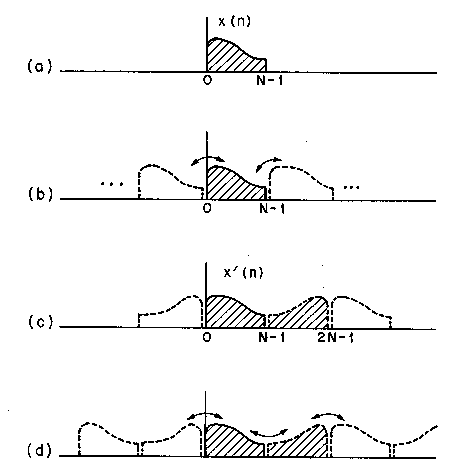
Figure TC.3.1.1 Illustration of end effects in DFT and DCT : (a) input block of length of N ; (b) end effects in DFT analysis/synthesis; (c) equivalent 2N-point data block for DCT; and (d) end effects in DCT analysis/synthesis [Tribolet and Crochiere, 1979, IEEE].
¡@
From the above discussion, it also follows that the DCT can be obtained with 2N log2N multiply-add operations. Slightly more efficient procedures are described in the literature [Chen, Smith and Fralick, 1976] [Wang, 1983].
¡@
Two-Dimensional DCT
In two dimensions, the DCT can be expressed in the form [Pratt, 1978] [Gonzalez and Wintz, 1977]
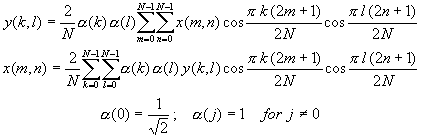
where x(m,n) is a N ¡ÑN field, k, l, m, n all range from 0 to N-1. Note that the transformation kernels are separable, so that the 2-D DCT can be conveniently performed in two steps, each of which involves a 1-D DCT. As in the one-dimensional case (Figure TC.3.1.1), DCT coding with an even symmetry end extension has fewer edge-effect problems than DFT image coding.