Introduction to Transform Coding

The techniques of the present chapter will represent another approach for the utilization of linear dependencies for efficient digitization, called Transform Coding (TC).

The asymptotic mse performance is theoretically the same for DPCM and TC [Nitadori, 1970]. However, important differences exist between DPCM and TC, especially at low bit rates: in terms of subjective quality, matching of inputs, TC is more robust than DPCM with regard to input statistics and channel errors [Netravali and Limb, 1980]. In the case of an ideal channel and a known source, TC offers a more direct approach to rate distortion bounds, in both image and speech applications. The price paid for these advantages is increased encoding with adaptive bit assignment (ATC), an encoding complexity comparable to that of fully adaptive predictive coding (APC).

Transform coding is a "frequency-domain" approach like sub-band coding (SBC). The number of transform coefficients will be called N; it will also be referred to as the order of the transform; transform coding is also referred to as block quantization [Huang and Schultheiss, 1963] and input blocks used for an Nth order transform will in fact be N samples long. By using appropriate values of N and appropriate bit allocation strategies, transform coding procedures for speech and images will be shown to provide high quality digitizations.

Transform Coding may also be used for the efficient encoding of sequences which are not successive samples of a waveform, but samples of N correlated sources: for example, the outputs of N parallel filters in a speech vocoder [Kramer and Mathews, 1956]. In all of the rest of this chapter, however, we will be concerned with the use of TC for encoding sequences of successive samples of a single waveform.

The efficiency of a transform coding system will depend on the type of linear transform and the nature of bit allocation for quantizing transform coefficients. Most practical systems will be based on sub-optimal approaches for transform operation as well as bit allocation.

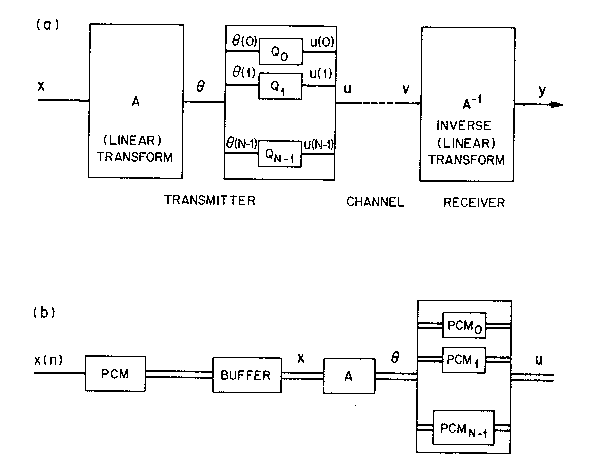
Figure TC.1.1(a) is a block diagram of transform coding. It is a waveform digitizing procedure where a block of N input samples x(n) is linearly transformed into a set of N transform coefficients y(n) (for example, a set of Fourier coefficients). The coefficients are then quantized for transmission, and a reconstruction of x(n) is obtained at the receiver using an inverse transform operation on quantized coefficients. Figure TC.1.1(b) shows how the above coding scheme is implemented. The input block could be one of high resolution PCM samples; for example, 8-bit resolution for images, and 12-bit resolution for speech. The output of the coder is the combination of the output of N PCM coders that convey quantized coefficient information, typically with a much lower total bit rate than what is present at the coder input.

Figure TC.1.1 (a) Block diagram of transform coding (TC); and (b) implementation of the encoder with a bank of PCM coders.

In principle, the set of N transform coefficients can be quantized with lower average mse by the use of vector quantization. A crucial part of Transform Coding is a bit-allocation algorithm that provides the possibility of quantizing some coefficients "frequency components" more finely than others. The criterion for bit allocation can be the minimization of the mean square value of reconstruction error. More generally, procedures may involve frequency-weighted reconstruction errors and adaptive bit-allocation for nonstationary inputs.

One-Dimensional Transforms

The input {x(n)} and output {y(n)} are one-dimensional sequence :

The transform is given by

where a(k, n) is a forward transformation kernel, and y(k) are the transform coefficients. The inverse transform that recovers the input sequence is

In matrix notation

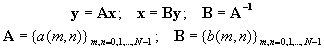
For simplicity, we use the notation

where the b_k are basis vectors.

Hence x is the weighted sum of basis vectors, where the weights are just the values of the transform coeffIcients (x can also be considered as a point in an N-dimensional y-space). In transform coding, output y will also be a weighted sum of basis vectors. But the weights will be quantized versions of y(k).

The matrix A can be complex in general, as in some later subsections. For the time being, let A be real; the class of orthogonal transforms is defined by

A^-1 = A^T

which implies that

A^TA = AA^T = I

where I is the identity matrix of order N. A real matrix is orthogonal if and only if its columns and rows form an orthonormal set. From the above, we find that the inverse transform is just the transpose of A:

B = A^-1 = A^T

This implies that the basis vectors are rows of A (see Figure TC.1.2) and that

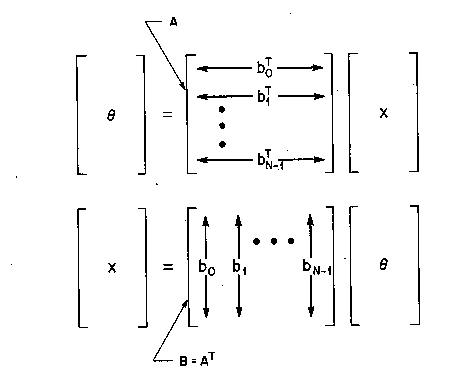
Figure TC.1.2 Transform matrix A, inverse B = A^-1 = A^T, and basis vectors b_k

Orthogonality is clearly a necessary property for basis vectors that are used to decompose an input into uncorrelated components in an N-dimensional space. Orthonormality of basis vector is a stronger property; it leads to transforms which are necessary in transform coding to make the average sum of the variances of the elements of y equal to s _x², the variance of the elements of x; this is also means that the average reconstruction error variance equals the error variance introduced in the quantization of transform coefficients.

Two-Dimensional transforms

Let us begin with a straightforward generalization

The above equations describe the transform of N²-point sequences with transformation kernels a(·) and b(·) that are described by N⁴ elements in general. For a 2-dimensional image input, the N² values of x(m, n) are usually the elements of a square array, a subimage of size N×N. Typical arrays in image coding use N = 4, 8, or 16. The partitioning into subimages is particularly efficient in cases where correlations are localized to neighboring pixels, and where structural details tend to cluster. The above equations do not preclude the arrangement of the same N² input points as a single (1×N²) vector.

Separable Two-Dimensional Transform Transforms. The image transforms will invariably assume a N×N square sub-image. In addition, we will only consider the simple case where the transform kernels a(·) and b(·) are separable into kernels signifying separate horizontal (row) and vertical (column) operations:

a ( k, l, m, n ) = a_v( k, m ) a_h( l, n )

b ( k, l, m, n ) = b_v( k, m ) b_h( l, n )

The two-dimensional transform to obtain y(k, l) can now be conveniently performed in two steps, each of which involves a one-dimensional transform operation. The first step uses a_h(·) for operation on row m to obtain the lth transform coefficient y(m, l), while the second step uses a_v(·) to provide the one-dimensional transform of column l:

X and Y are arrays which have as their elements x(m, n) and y(k, l), respectively.

A_h = { a_h(m,n) }_{m,n=0,1,...,N-1} ; A_v = { a_v(m,n) }_{m,n=0,1,...,N-1}

so that

Y = A_vXA_h^T

For symmetrical kernels,

A_v = A_h = A ; Y = AXA^T

and with A^-1 = A^T,

X = A^TYA

Note that A is simply the 1-D transform and that the matrix operation of the above equation is possible only with separable transforms. Wit general non-separable transforms, 2-D operations would involve tensor operations, rather than the matrix operations of the above equation. Also, as a result of a separable b(·) kernel, image X can be expressed as a superposition of basis images B_kl

The second part of the above equation is a good working definition for a separable transform.

The basis image is the two-dimensional counterpart of the basis vector in the 1-D transforms. In transform coding, the reconstructed image Y will be superposition of basis images B_kl which have been weighted by quantized versions of y(k, l ):