Computer Organization and Structure

Homework #3

Due: 2004/11/9

1. Convert 4096_ten, -2,047_ten, and -2,000,000_ten into 32-bit two’s complement binary numbers, respectively, and convert the following two’s complement binary numbers to be decimal numbers:

a. 1111 1111 1111 1111 1111 1111 0000 0110_two;

b. 1111 1111 1111 1111 1111 1111 1110 1111_two;

c. 0111 1111 1111 1111 1111 1111 1110 1111_two.

2. Suppose that all of the conditional branch instructions except beq and bne were removed from the MIPS instruction set along with slt and all of its variants (slti, sltu, sltui). Show how to perform

slt $t0, $s0, $s1

using the modified instruction set in which slt is not available. (Hint: It requires more than two instructions.)

3. The ALU supported set on less than (slt) using just the sign bit of the adder. Let’s try a set on less than operation using the values -7_ten and 6_ten. To make it simpler to follow the example, let’s limit the binary representations to 4 bits: 1001_two and 0110_two.

1001_two – 0110_two = 1001_two + 1010_two = 0011_two

This result would suggest that -7_ten > 6_ten, which is clearly wrong. Hence we must factor in overflow in the decision. Modify the 1-bit ALU in the following figures to handle slt correctly.

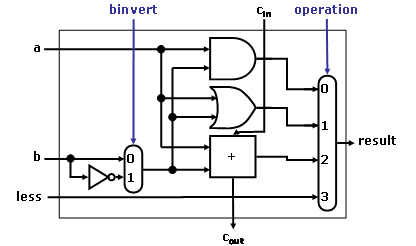
Figure 1: A 1-bit ALU that performs AND, OR, and addition on a and b or b’.

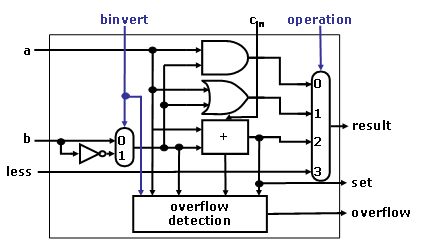
Figure 2: A 1-bit ALU for the most significant bit.

4. Add 2.85_ten x 10³ to 9.84_ten x 10⁴ and add 3.63_ten x 10⁴ to 6.87_ten x 10³, respectively, assuming that you have only three significant digits, first with guard and round digits and then without them.

5. Show the IEEE 754 binary representation for the floating-point numbers 20_ten, 20.5_ten, 0.1_ten, and -5/6, respectively.